Question

9. Luke is an astronaut that moves his position in the space shuttle by climbing a

3.0 m ladder in 5.0 seconds at Cape Kennedy (g = 9.8 m/s^2). After landing on the
moon (g = 1.6 m/s^2), Luke climbs a 3.0 m ladder in 5.0 seconds to begin the trip back to Earth. Is more power expended by the astronaut on Earth or on the moon, and by what factor?

Answer 1

Step-by-step explanation:

Remember that power is defined as how much Work is done per unit of time.

`P = (dW)/(dt)`

Work is defined as the amount of force applied across a certain distance.

`W = F*d`

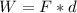
Since in both cases of climbing the ladder (on Earth and the moon), Luke coveres the same amount of distance in the same amount of time, we are only left with one difference between the two cases - gravity.

If you were to carry your backpack on the moon with the same load of text books, it would take less force to pick it up on the moon. Therefore, Luke expends less effort on the environment with less gravity - the moon.

To find the difference factor - you would want to divid the gravitational contants between earth and the moon.

Answer 2

It takes 6.125 times as much work on Earth as it does on the moon.

Step-by-step explanation:

Formulas

The power formula is

P = Work / Time

Work = Force * distance

Givens

d = 3.0 meters

t = 5.0 seconds

g = 9.8 m/s^2 on earth

g = 1.8 m/s^2 on the moon

Solution

Earth

Work = F * d

Work = m* a * 3.0 m

Work = m *9.8 * 3.0

Work = m * 29.4

Power = (Work * 29.4)/5

Power = 29.4/5 * m

Power = 5.88 watts.

Moon

You follow the same procedure except you use 1.6 for a.

Work = m * 1.6 * 3

Work = 4.8*m Joules

Power = 4.8 * m/ 5

Power = 0.96 * m Watts

P_earth/Power_moon = 5.88 * m / 0.96 * m = 6.125

Power =