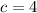Answer:
A)
Explanation:
First we will graph th parent function which is a cube root and we can see it in the attachment #1.
In this excercise there are two types of transformations of the parent function:
![f(x)=\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/high-school/a1v3umosxss7mpgi39xzzne7jucatjz2jy.png)
First:
 shifts the function b units to the left.(Attachment #2 )
shifts the function b units to the left.(Attachment #2 )
![f(x)=\sqrt[3]{x+2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/y15l1mjvvsrj3dlpw0flhrpdgnuq9y06ds.png)
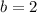
Second:
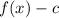 shifts the function c units downward. (Attachment #3)
shifts the function c units downward. (Attachment #3)
![f(x)=\sqrt[3]{x+2}+4](https://img.qammunity.org/2020/formulas/mathematics/high-school/gydul6pz5j17o7bh6v143ycrnaojhr3p41.png)