Question

(HELP ASAP PLEASE!!)

Two brothers went shopping at a back-to-school sale where all shirts were the same price, and all the shorts too. The younger brother spent $79 on 4 new shirts and 3 pairs of shorts. The older brother purchased 7 new shirts and 8 pairs of shorts and paid a total of $185. How much did each item cost?

Each shirt cost $ ___ and each pair of shorts cost $ ___ .

Answer 1

Shirts = $7

Shorts $17

Explanation:

Let:

T - shirts

S - shorts

We can make two equations out of this problem:

4T + 3S = $79

7T + 8S = $185

Through substitution we can solve for one of the unknowns. We make one equation to solve for an unknown

`4T+3S=\$79\\\\3S = \$79-4T\\\\S=(\$79-4T)/(3)`

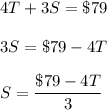
We use the formula of S and insert it into the other equation:

`7T+8((\$79-4T)/(3)) = \$185\\\\7T + (\$632-32T)/(3)=\$185\\\\(\$632-32T)/(3)=\$185-7T\\\\\$632-32T=3(\$185-7T)\\\\$632-32T=\$555 - 21T\\\\-32T+21T=\$555-\$632\\\\-11T=-\$77\\\\(-11T)/(11)=(-\$77)/(11)\\\\T = \$7`

Thus T-shirts are $7 each.

Now that we know T, we can use it to solve for the other unknown. You can use it on any of the formulas.

`4T+3S=\$79\\\\4(\$7) + 3S = \$79\\\\\$28+3S =\$79\\\\3S=\$79-\$28\\\\3S=\$51\\\\S=(\$51)/(3)\\\\S = \$17`

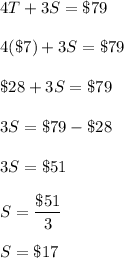
We know then that Shorts are $17 each.