Question

John drew a right triangle with sides 6 inches , 8inches , and 10 inches long what is the area of the triangle ?

Answer 1

24 in²

Explanation:

The easy way:

The two legs, or shorter sides, of a right triangle form that triangle's base and height. Knowing that the area of a triangle is
`(bh)/(2)` (where b is the base and h is the height), we can use the 6 inch leg for the base and the 8 inch leg for the height to find an area of
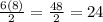`(6(8))/(2)=(48)/(2)=24` in².

The harder but more general way

There's a nice formula for calculating the area of any triangle given its side lengths found by this Greek guy named Heron, and it's appropriately called Heron's formula:

`A=\sqrt{s(s-a)(s-b)(s-c)`

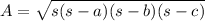
a, b, and c are the lengths of triangle, and s here is half the triangle's perimeter (also called the semi-perimeter), or mathematically:

`s=(a+b+c)/(2)`

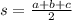
For our problem, let's pick a = 6, b = 8, and c = 10. This would give us

`s=(6+8+10)/(2) =(24)/(2)=12`

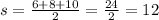
Substituting that s back into Heron's formula, we get

`A=√(12(12-6)(12-8)(12-10))=√(12(6)(4)(2))\\=√(72(8))=√(576)=24`

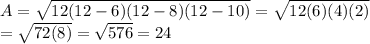
So our area is 24 in²