The surface area of the sphere is given by the equation
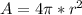 ,
,
where A is the surface area and r is the radius.
We want to find the volume of the sphere, which is given by the equation
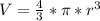 ,
,
where V is the volume and r is the radius.
Looking at these equations, we see that they both involve the sphere's radius. If we know what r is, we can calculate the volume.
We know that the sphere's surface area is
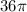 . Plugging that in for A in the surface area equation, we get
. Plugging that in for A in the surface area equation, we get
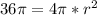 , then divide by
, then divide by

 , then divide by 4
, then divide by 4
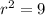 , then take the square root of both sides
, then take the square root of both sides
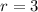
So the radius of the sphere is 3. Plugging this into the volume equation,
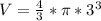 , simplify terms
, simplify terms
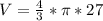 , multiply
, multiply
 by 27
by 27
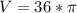
So the volume of the sphere is
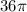 .
.