Question

Which of the following statements are true?

Answer 1

option A and B are correct.

Explanation:

Given:
`p(t) = (64)/(1 + 11e^(-.08t) )`

Option A:
`\lim_(t \to \infty) (64)/(1 + 11e^(-.08(\infty)) )  = (64)/(1 + 0)  = 64`

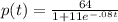
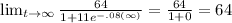
Option A is true,

Option B:
`P(0) = (64)/(1 + 11)  = 5.33`

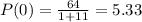
Option B is also true.

Option C:

`P(t + 1) = (64)/(1 + 11e^(-.08(t + 1)) )  = (64)/(1 + 10.15e^(-.08t) ) \\1.08 · P(t) = (64 · 1.08 )/(1 + 11e^(-.08t) )   = (69.12)/(1 + 11e^(-.08t) )`

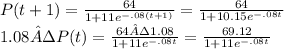
P(t + 1) ≠ 1.08 · P(t)

Option C is incorrect.

Option D: It is also incorrect, because according to option 2 earth's population will not grow exponentially without Bound.