Question

Suppose the initial height of a Pumpkin is 12 feet and the pumpkin is being launched with a velocity of 61 feet per second. Use this information to find out the maximum height the pumpkin will go before landing.

Please show your work

(98 points)

Answer 1

Hello!

The answer is:

The maximum height before landing will be 69.7804 feet.

Why?

Since there is no information about the angle of the launch, we can safely assume that it's launched vertically.

So, we can calculate the maximum height of the pumpkin using the following formulas:

`y=y_o+v_(o)*t-(1)/(2)gt^(2)`

`v=vo-gt`

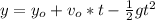
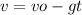
Where,

y, is the final height

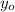`y_o`, is the initial height

g, is the acceleration of gravity , and it's equal to:

`g=32.2(ft)/(s^(2) )`

t, is the time.

Now, we are given the following information:

`y_(o)=12ft\\\\v=61(ft)/(s)`

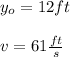
Then, to calculate the maximum height, we must remember that at the maximum height, the speed tends to 0, so, calculating we have:

Time calculation,

We need to use the following equation,

`v=vo-gt`

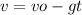
So, substituting we have:

`v=61(ft)/(s)-32.2(ft)/(s^(2))*t\\\\-61(ft)/(s)=-32.2(ft)/(s^(2))*t\\\\t=\frac{-61{ft}{s}}{-32.2(ft)/(s^(2))}=1.8944s`

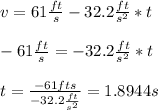
We know that it will take 1.8944 seconds to the pumpkin to reach its maximum height.

Maximum height calculation,

Now, calculating the maximum height, we need to use the following equation:

`y=y_o+v_(o)*t-(1)/(2)gt^(2)`

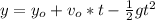
Substituting and calculating, we have:

`y=y_o+v_(o)*t-(1)/(2)gt^(2)`

`y=12ft+61(ft)/(s)*1.8944s-(1)/(2)32.2(ft)/(s^(2))*(1.8944s)^(2)`

`y=12ft+61(ft)/(s)*1.8944s-(1)/(2)32.2(ft)/(s^(2))*(1.8944s)^(2)\\\\y_(max)=12ft+115.5584ft-16.1(ft)/(s^(2))*(3.5887s^(2))\\\\y_(max)=127.5584ft-57.7780ft=69.7804ft`

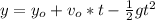
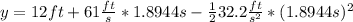
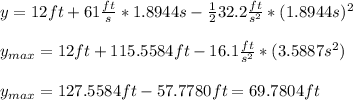
Hence, we have that the maximum height before the landing will be 69.7804 feet.

Have a nice day!