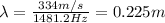Question

A sound source A and a reflecting surface B move directly toward each other. Relative to the air, the speed of source A is 28.7 m/s, the speed of surface B is 62.2 m/s, and the speed of sound is 334 m/s. The source emits waves at frequency 1110 Hz as measured in the source frame. In the reflector frame, what are (a) the frequency and (b) the wavelength of the arriving sound waves? In the source frame, what are (c) the frequency and (d) the wavelength of the sound waves reflected back to the source?

Answer 1

(a) 1440.5 Hz

The general formula for the Doppler effect is

`f'=((v+v_r)/(v+v_s))f`

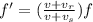
where

f is the original frequency

f is the apparent frequency

`v` is the velocity of the wave

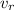`v_r` is the velocity of the receiver (positive if the receiver is moving towards the source, negative otherwise)

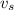`v_s` is the velocity of the source (positive if the source is moving away from the receiver, negative otherwise)

Here we have

f = 1110 Hz

v = 334 m/s

In the reflector frame (= on surface B), we have also

`v_s = v_A = -28.7 m/s` (surface A is the source, which is moving towards the receiver)

`v_r = +62.2 m/s` (surface B is the receiver, which is moving towards the source)

So, the frequency observed in the reflector frame is

`f'=((334 m/s+62.2 m/s)/(334 m/s-28.7 m/s))1110 Hz=1440.5 Hz`

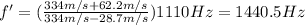
(b) 0.232 m

The wavelength of a wave is given by

`\lambda=(v)/(f)`

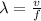
where

v is the speed of the wave

f is the frequency

In the reflector frame,

f = 1440.5 Hz

So the wavelength is

`\lambda=(334 m/s)/(1440.5 Hz)=0.232 m`

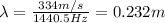
(c) 1481.2 Hz

Again, we can use the same formula

`f'=((v+v_r)/(v+v_s))f`

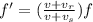
In the source frame (= on surface A), we have

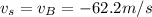`v_s = v_B = -62.2 m/s` (surface B is now the source, since it reflects the wave, and it is moving towards the receiver)

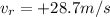`v_r = +28.7 m/s` (surface A is now the receiver, which is moving towards the source)

So, the frequency observed in the source frame is

`f'=((334 m/s+28.7 m/s)/(334 m/s-62.2 m/s))1110 Hz=1481.2 Hz`

(d) 0.225 m

The wavelength of the wave is given by

`\lambda=(v)/(f)`

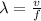
where in this case we have

v = 334 m/s

f = 1481.2 Hz is the apparent in the source frame

So the wavelength is

`\lambda=(334 m/s)/(1481.2 Hz)=0.225 m`