Question

Which choice is equivalent to the fraction below when x is greater than or equal to 1?

Please show work.

Answer 1

Answer: B

Explanation:

Answer 2

B. √{x} + √{x - 1}

Explanation:

As hinted in the question, we have to simplify the denominator.

To understand it easier, let's imagine we have x - y in the denominator. If we multiply it with x + y we'll get x² - y², right? Check the next line:

(x - y) (x + y) = x² + xy -xy - y² = x² - y²

If we have the square of those nasty square roots, it will be much simpler to deal with. So, let's multiply the initial fraction using x+y, but with the real values:

`(1)/(√(x) - √(x - 1) ) * (√(x) + √(x - 1))/(√(x) - √(x - 1)) = (√(x) + √(x - 1))/((√(x) )^(2) - (√(x - 1) )^(2) )`

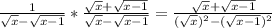
Then we simplify:

`(√(x) + √(x - 1))/((√(x) )^(2) - (√(x - 1) )^(2) ) = (√(x) + √(x - 1))/((x) - (x - 1) ) = (√(x) + √(x - 1))/( 1 )`

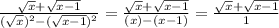
So, the answer is B. √{x} + √{x - 1}