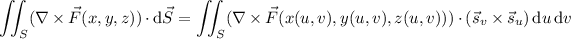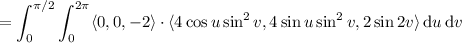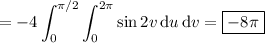As near as I can tell, you're given the vector field

and that
 is the part of the upper half of the sphere with equation
is the part of the upper half of the sphere with equation
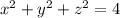
with boundary
 the circle in the plane
the circle in the plane
 .
.
Parameterize
 by
by
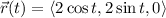
with
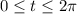 . Then the line integral of
. Then the line integral of
 along
along
 is
is
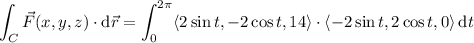
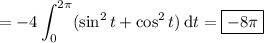
Parameterize
 by
by
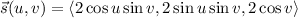
with
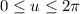 and
and
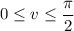 . We have
. We have
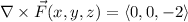
Take the normal vector to
 to be
to be
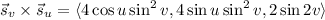
Then the surface integral of the curl of
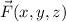 across
across
 is
is