Question

Please help me thank you

Answer 1

solution for #18 is C and for #19 is D

Answer 2

QUESTION 18

Use the Pythagorean Identity.

`\cos^(2)( \theta) +\sin^(2)( \theta) = 1`

We substitute the given value into the formula,

`\cos^(2)( \theta) +( { (4)/(7) })^(2) = 1`

`\cos^(2)( \theta) + (16)/(49) = 1`

`\cos^(2)( \theta) = 1 - (16)/(49)`

`\cos^(2)( \theta) = (33)/(49)`

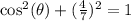
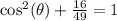
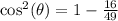
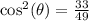
Since we are in the first quadrant, we take positive square root,

`\cos( \theta) = \sqrt{(33)/(49) }`

`\cos( \theta) = ( √(33))/(7)`

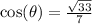
The 3rd choice is correct.

QUESTION 19.

We want to simplify;

`18 \sin( \theta) \sec( \theta)`

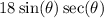
Recall the reciprocal identity

`\sec( \theta) = (1)/( \cos( \theta) )`

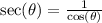
This implies that,

`18 \sin( \theta) \sec( \theta) =18 \sin( \theta) * (1)/( \cos( \theta) )`

`18 \sin( \theta) \sec( \theta) =18 * (\sin( \theta) )/( \cos( \theta) )`

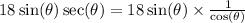
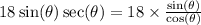
This will give us:

`18 \sin( \theta) \sec( \theta) =18 \tan( \theta)`

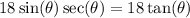
The correct choice is D.