Question

1. Consider the function f(x) = x2 + 2x - 8.

(a) What are the x-intercepts of the graph of the function?
(b) What is the equation of the axis of symmetry? Explain how you know.
(c) What is the vertex of the function? Show your work.
(d) What is the domain of the function? Use set notation (i.e. x )
(e) What is the range of the function? Use set notation (i.e. y )
(f) Graph the function.

Answer 1

a)The x-intercepts are:

(-4,0) and (2,0)

b) The axis of symmetry is x=-1

c) The vertex of this function is (-1,-9)

d)Domain: {
`x|x \in \: R`}

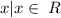e) Range : {
`y |y \geqslant - 9`}

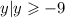Step-by-step explanation

The given function is:

`f(x) = {x}^(2) + 2x - 8`

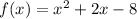
We complete the square to write this function in the form:

`f(x)=a{(x - h)}^(2) + k`

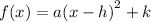
We add and subtract the square of half the coefficient of x.

`f(x) = {x}^(2) + 2x + {1}^(2) - {1}^(2) - 8`

`f(x) = {(x + 1)}^(2) - 9`

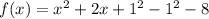
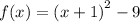
The vertex of this function is (h,k) which is (-1,-9)

The equation of axis of symmetry is x=h

But h=-1, hence the axis of symmetry isx=-1

To find the x-intercepts, we put f(x)=0

`{(x + 1)}^(2) - 9 = 0`

`{(x + 1)}^(2) = 9`

`x + 1= \pm √(9)`

`x= - 1 \pm3`

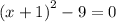
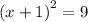
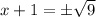
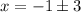
x=-4, 2

The x-intercepts are:

(-4,0) and (2,0)

The given function is a polynomial function, the domain is all real numbers.

`x|x \in \: R`

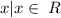
e) The function has a minimum value of y=-9.

Therefore the range is

`y |y \geqslant - 9`

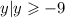
Using the intercepts and vertex we can now draw this graph easily.

The graph of this function is shown in the attachment.