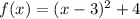Answer:
The vertex form of a quadratic equation is:
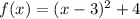
the minimum value of f(x) is
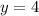
Explanation:
Given a quadratic equation of the form
 then the x coordinate of the vertex is
then the x coordinate of the vertex is
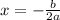
So for

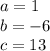
Therefore
The x coordinate of the vertex is:


The y coordinate of the vertex is:
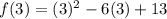

By definition the minimum value of the quadratic function is the same as the coordinate of y of its vertex
So the minimum value is
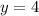
The vertex form of a quadratic equation is:
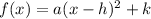
Where
a is the main coefficient.

h is the x coordinate of the vertex.
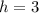
k is the y coordinate of the vertex.
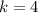
So the vertex form of a quadratic equation is: