Question

Please help me with these 2 questions thank you so much #17 and #18

Answer 1

#17: Domain: [−4,∞),x≥−4

Range: [−2,∞),y

#18 g(2)=4(2)+2

g(2)=10

f(10)=3(10)^2-2

f(10)=298

Answer 2

For this case we have:

Question 1:

We have the following functions:

`f (x) = 2x-1\\g (x) = x ^ 2-2`

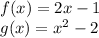
We must find (g_ {0} f) (x).

By definition of composition of fusions we have to:

`(g_ {0} f) (x) = g [f (x)]\\(g_ {0} f) (x) = g [2x-1]\\(g_ {0} f) (x) = (2x-1) ^ 2-2\\(g_ {0} f) (x) = 4x ^ 2-2 (2x) + 1-2\\(g_ {0} f) (x) = 4x ^ 2-4x-1`

Answer:

`(g_ {0} f) (x) = 4x ^ 2-4x-1`

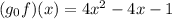
Question 2:

For this case we have a function of the form
`y = f (x)`, where:
`f (x) = \sqrt {x + 4} -2`

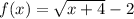
We must graph the given function.

By definition, the domain of the function will be given by the values for which the function is defined. The function is not defined when the root is negative, that is to say for values of "x" less than -4. Then, the domain is:

[-4, ∞)

For its part, the range is the set of values that correspond to the domain. When replacing the values from -4 to infinity we have the following range:

[-2, ∞)

Answer:

See attached image

Domain: [-4, ∞)

Range: [-2, ∞)

Question 3:

For this case we have the following functions:

`f (x) = 3x ^ 2-2\\g (x) = 4x + 2`

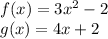
We must find, (f + g) (x):

By definition, we have to:

`(f + g) (x) = f (x) + g (x)\\(f + g) (x) = 3x ^ 2-2 + (4x + 2)\\(f + g) (x) = 3x ^ 2-2 + 4x + 2\\(f + g) (x) = 3x ^ 2 + 4x`

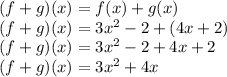
Now, we must find
`(f + g) (2):`

`(f + g) (2) = 3 (2) ^ 2 + 4 (2)\\(f + g) (2) = 3 (4) +4 (2)\\(f + g) (2) = 12 + 8\\(f + g) (2) = 20`

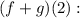
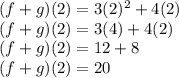
Answer:

`(f + g) (2) = 20`