Question

In 1990, the rate of change of the world population was approximately 0.09125 billion per year (or approximately 1 million people every four days). The world population was estimated to be 5.3 billion in 1990.

Write an equation to model the population, P (in billions), in terms of t, where t is the number of years since 1990 (t = 0 corresponds to 1990)

A. P= 5.3 + 0.09125t

B. P= 5.3t + 0.09125

C. P= -5.3 + 0.09125t

D.P= -5.3t + 0.09125

Answer 1

Answer: Option A

`P = 5.3 + 0.09125t`

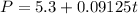
Explanation:

Note that for the initial year, 1990, the population was 5.3 billion.

The exchange rate is 0.09125 billion per year. In other words, each year there are 0.09125 billion more people.

In year 2 there will be 0.09125 * 2 billion people

In year 3 there will be 0.09125 * 3 billion people

In year 4 there will be 0.09125 * 4 billion people

In year t there will be 0.09125 * t billion of people

So the equation that models the number of people that there will be as a function of time is:

`P = P_0 + rt`

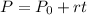
Where
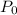`P_0` is the initial population

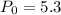`P_0 = 5.3` billion

r is the rate of increase

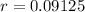`r = 0.09125` billion per year

finally the equation is:

`P = 5.3 + 0.09125t`

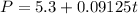
The correct answer is option A.