Question

Please help me thank you

Answer 1

option C Only second equation is an identity is correct.

Explanation:

1)

`1 +(cos^2\theta)/(cot^2\theta(1-sin^2\theta))= 9 sec^2\theta`

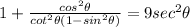
We need to prove this identity.

We know:

`cos^2\theta + sin^2\theta = 1\\=> cos^2\theta = 1- sin^2\theta`

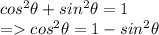
and

`(1)/(cot^2\theta ) = tan^2\theta \\and\\tan^2\theta = (sin^2\theta)/(cos^2\theta)`

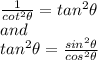
Using these to solve the identity

`1 +(cos^2\theta)/(cot^2\theta(cos^2\theta))= 9 sec^2\theta\\1 +(1)/(cot^2\theta) = 9 sec^2\theta\\1+tan^2\theta = 9 sec^2\theta\\1+(sin^2\theta)/(cos^2\theta) = 9sec^2\theta\\\\(cos^2\theta+sin^2\theta)/(cos^2\theta) = 9sec^2\theta\\(1)/(cos^2\theta)=9sec^2\theta \\sec^2\theta \\eq 9sec^2\theta`

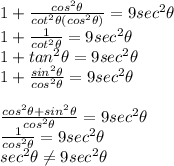
So, this is not an identity.

2)

`20sin\theta((1)/(sin\theta) -(cot\theta)/(sec\theta)) =20sin^2\theta\\`

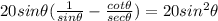
We need to prove this identity.

We know:

`cot\theta = (cos\theta)/(sin\theta) \\and \\sec\theta=(1)/(cos\theta) \\so,\,\, (cot\theta)/(sec\theta)= ((cos\theta)/(sin\theta))/((1)/(cos\theta))  \\Solving\\ (cot\theta)/(sec\theta) =(cos^2\theta)/(sin\theta)`

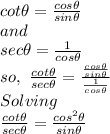
Using this to solve the identity

`20sin\theta((1)/(sin\theta) -(cot\theta)/(sec\theta)) =20sin^2\theta\\\\Putting\,\,values\,\,\\ 20sin\theta((1)/(sin\theta) -(cos^2\theta)/(sin\theta)) =20sin^2\theta\\ 20sin\theta((1-cos^2\theta)/(sin\theta)) =20sin^2\theta\\1-cos^2\theta = sin^2\theta\\ 20sin\theta((sin^2\theta)/(sin\theta)) =20sin^2\theta\\Cancelling\,\, sin\theta \,\,over \,\,sin\theta\\20sin^2\theta=20sin^2\theta`

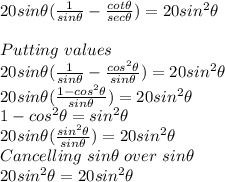
So, this is an identity.

So, option C Only second equation is an identity is correct.