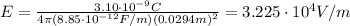Question

A spherical capacitor contains a charge of 3.10 nC when connected to a potential difference of 250 V. If its plates are separated by vacuum and the inner radius of the outer shell is 4.00 cma)Calculate the capacitance: found to be 1.24*10^-11 Fb)Find the radius of the inner spere: found to be .0294mc)Calculate the electric field just outside the surface of the inner sphere. T

Answer 1

(a)
`1.24\cdot 10^(-11) F`

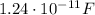
The general formula for the capacitance of a capacitor is:

`C=(Q)/(V)`

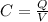
where

Q is the charge stored on the capacitor

V is the potential difference across the capacitor

In this problem, we have

`Q=3.10 nC = 3.10\cdot 10^(-9) C` is the charge stored

V = 250 V is the potential difference

Substituting, we find

`C=(3.10\cdot 10^(-9)C)/(250 V)=1.24\cdot 10^(-11) F`

(b) 0.0294 m

The capacitance of a spherical capacitor is given by

`C=(4\pi \epsilon_0)/((1)/(a)-(1)/(b))`

where

a is the radius of the inner shell

b is the radius of the outer shell

Here we have

b = 4.00 cm = 0.04 m

and the capacitance is

`C=1.24\cdot 10^(-11) F`

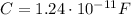
So we can re-arrange the equation to find a, the radius of the inner sphere:

`a=((4\pi \epsilon_0)/(C)+(1)/(b))^(-1) =((4\pi (8.85\cdot 10^(-12)F/m))/(1.24\cdot 10^(-11)F)+(1)/(0.04 m))^(-1)=0.0294 m`

(c)
`3.225 \cdot 10^4 V/m`

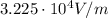
The electric field just outside the surface of the inner sphere with charge Q is equal to the electric field produced by a single point charge Q at a distance of r = a:

`E=(Q)/(4\pi \epsilon_0 a^2)`

where

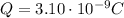`Q=3.10 \cdot 10^(-9) C` is the charge on the sphere

a = 0.0294 m is the radius of the inner sphere

Substituting the data into the formula, we find:

`E=(3.10\cdot 10^(-9)C)/(4\pi (8.85\cdot 10^(-12)F/m) (0.0294 m)^2)=3.225 \cdot 10^4 V/m`