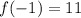Question

Determine whether f(x) = -5x2 - 10x + 6 has a maximum or a minimum

value. Find that value and explain how you know.

Answer 1

The function has a maximum

The maximum value of the function is

`f (-1) = 11`

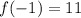
Explanation:

For a quadratic function of the form:

`ax ^ 2 + bx + c` where a, b and c are the coefficients of the function, then:

If
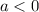`a <0` the function has a maximum

If
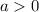`a> 0` the function has a minimum value

The minimum or maximum value will always be at the point:

`x=-(b)/(2a)\\\y=f(-(b)/(2a))`

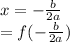
In this case the function is:
`f(x) = -5x^2 - 10x + 6`

Note that

`a = -5,\ a <0`

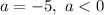
The function has a maximum

The maximum is at the point:

`x=-(-10)/(2(-5))`

`x=-1`

`y=f(-1)`

`y= -5(-1)^2 - 10(-1) + 6`

`y= 11`

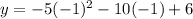
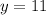
The maximum value of the function is

`f (-1) = 11`