Question

What is the area of the figure? Make sure to show your work and provide complete geometric explanations.

Answer 1

`Area = 144 {ft}^(2)`

EXPLANATION

We use the sine ratio to find the missing side.

`\sin(45 \degree) = (AC)/(24)`

`24\sin(45 \degree) = AC`

`AC = 24 * ( √(2) )/(2)`

`AC = 12 √(2) ft`

The triangle is a right isosceles triangle.

This implies that,

AC=BC=12√2 ft.

The area of the triangle is:

`Area = (1)/(2) bh`

We substitute the values to get,

`Area = (1)/(2) * 12 √(2) * 12 √(2)`

`Area = 144 {ft}^(2)`

Answer 2

`A = 144\ ft`

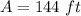
Explanation:

The area of a triangle is:

`A = 0.5b*h`

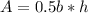
Where b is the base of the triangle and h is the height

In this case we know the hypotenuse of the triangle and the angle B.

Then we can use the sine of the angle to find the side opposite the angle

By definition we know that

`sin (\theta) = (opposite)/(hypotenuse)`

In this case hypotenuse = 24

opposite = b

Then:

`sin (45) = (b)/(24)`

`b= 24*sin(45)`

`b=12√(2)`

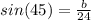
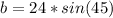
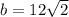
Now

`cos(\theta) = (adjacent)/(hypotenuse)`

adjacent = a = h

`cos(45) = (h)/(24)`

`h = 24*cos(45)\\\\h=12√(2)`

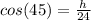
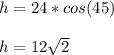
Then the area is:

`A = 0.5*12√(2)(12√(2))\\\\A=144\ ft`