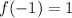Answer:
Explanation:
Given
f(x) =
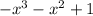
Finding f(-1) means, we have to put -1 in the places of x in the function,
So, putting x=-1 in the function
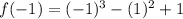
As the power 3 is odd, the minus will remain the same, while in the 2nd term minus will be eliminated due to even power. So,
=>
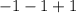
=> 1
Hence,