Question

In 1909 Robert Millikan was the first to find the charge of an electron in his now-famous oil drop experiment. In the experiment tiny oil drops are sprayed into a uniform electric field between a horizontal pair of oppositely charged plates. The drops are observed with a magnifying eyepiece, and the electric field is adjusted so that the upward force q E on some negatively charged oil drops is just sufficient to balance the downward force m g of gravity. Millikan accurately measured the charges on many oil drops and found the values to be whole-number multiples of 1.6 × 10−19 C — the charge of the electron. For this he won the Nobel Prize. If a drop of mass 1.51837 × 10−12 kg remains stationary in an electric field of 1 × 106 N/C, what is the charge on this drop? The acceleration due to gravity is 9.8 m/s 2 . Answer in units of C.

Answer 1

`1.49\cdot 10^(-17)C`

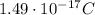
Step-by-step explanation:

The oil drop remains stationary when the electric force on it and the gravitational force are balanced, so we have:

`F_E = F_G\\qE = mg`

where

q is the charge of the oil drop

E is the electric field strength

m is the mass of the drop

g is the acceleration due to gravity

here we have

`E=1\cdot 10^6 N/C`

`m=1.51837\cdot 10^(-12) kg`

`g=9.8 m/s^2`

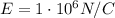
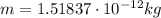
So the charge of the drop is

`q=(mg)/(E)=((1.51837\cdot 10^(-12) kg)(9.8 m/s^2))/(1\cdot 10^6 N/C)=1.49\cdot 10^(-17)C`