Question

Which linear inequality is represented by the graph?

Answer 1

the answer is b

Explanation:

Answer 2

The linear inequality is
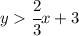`y > \cfrac 23 x+3`, which is the third option.

Explanation:

In order to determine the inequality, we need to first identify the line equation associated to it, to do that we can identify a couple of points and get the slope then the line equation.

Identifying points and finding slope.

From the segmented line we can tell that it crosses the points (0,3) and (3, 5), thus we can find the slope using

`m = \cfrac{y_2-y_1}{x_2-x_1}`

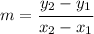
Replacing the points we get

`m= \cfrac{5-3}{3-0}`

`m = \cfrac 23`

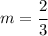
Writing the line equation.

Now that we have the slope m, and a point (0,3) we can find the line equation using,

`y-y_1 = m(x-x_1)`

Replacing the point and slope we get

`y-3 = \cfrac 23 (x-0)`

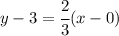
Simplifying and solving for y we get

`y = \cfrac 23 x+3`

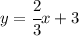
Writing the inequality.

Notice that the associated line is a segmented line, so the linear inequality does not contain it that is why we only need to use greater than or less symbols.

Then we can tell that the shaded area is above the segmented line so we can conclude that the linear inequality is

`y > \cfrac 23 x+3`,

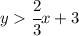And that is the third option.