Answer:
The function is:

Explanation:
If we have a function f(x) and we want to compress its graph vertically c units then we must do the transformation
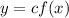 Where
Where
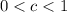 .
.
If we want to make a transformation that moves horizontally h units the graph of f(x) then we must do:

If
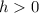 the graph of f(x) shifts h units to the left
the graph of f(x) shifts h units to the left
If
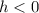 the graph of f(x) shifts h units to the right.
the graph of f(x) shifts h units to the right.
If we want to make a transformation that moves vertically k units the graph of f(x) then we must do
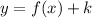
If
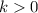 the graph of f(x) moves k units up
the graph of f(x) moves k units up
If
 the graph of f(x) shifts k units down
the graph of f(x) shifts k units down
In this case
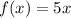
If the transformation vertically compresses the function by a factor of
 and moves the function 3 units to the right and 2 units up then the transformation is:
and moves the function 3 units to the right and 2 units up then the transformation is:
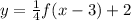
The function is:
