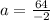Question

A line passes through A(3, 7), and B(-4, 9). Find the value of a if C(a, 1) is on the line.

Answer 1

a=-32

Explanation:

Answer 2

a=-32

EXPLANATION

If C(a,1) is on the line that passes through A(3, 7), and B(-4, 9), then the three points are collinear.

This implies that, when we find the slope using any two points, we should get the same result.

`(9 - 1)/( - 4 - a) = (9 - 7)/( - 4 - 3)`

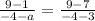
We simplify to obtain;

`(8)/( - 4 - a) = ( - 2)/( - 7 )`

`(8)/( - 4 - a) = ( 2)/( 7 )`

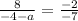
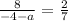
We cross multiply to get;

`8 * 7 = 2( - 4 - a)`

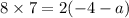
This implies that,

`56 = - 8 - 2a`

`56 + 8= - 2a`

`64 = - 2a`

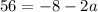
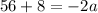
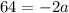
Divide both sides by -2

`a = (64)/( - 2)`

`a = - 32`