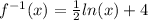Question

F(x)=e^2x-4
Determine inverse of given function

Answer 1

`f^(-1)(x)=(1)/(2)ln(x)+2`

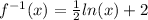
Explanation:

Start by changing the f(x) into a y. Then switch the x and the y. Then solve for the new y. Like this:

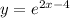`y=e^(2x-4)` becomes

`x=e^(2y-4)`

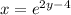
To solve for the new y, we need to get it out of its current exponential position which requires us to take the natural log of both sides. Since a natural log has a base of e, natural logs and e's "undo" each other, just like taking the square root of a squared number.

`ln(x)=ln(e)^(2y-4)`

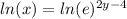
When the ln and the e cancel out we are left with

ln(x) = 2y - 4. Add 4 to both sides to get

ln(x) + 4 = 2y. Divide both sides by 2 to get

`(1)/(2)ln(x) + 4 = y`.

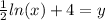Since that is the inverse of y, we can change the y into inverse function notation:

`f^(-1)(x)=(1)/(2)ln(x)+4`