Question

Find the distance on the coordinate system from the point (-3,4)to the point (8,-7)Find

Answer 1

Let's say point A is (-3,4) and point B is (8,-7).

The x-distance from A to B is -3 to 8. This is equivalent to the expression
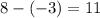`\abs{8 - (-3)} = \abs{11}`. So the x-distance is 11.

The y-distance from A to B is 4 to -7. This is equivalent to the expression
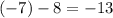`\abs{(-7) - 8} = \abs{-13}`. So the y-distance is 13. We take the absolute value because distance is always positive, and is never negative.

The x- and y-distances create a right triangle. So, we can apply the Pythagoren Theorem:
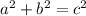`a^(2)+b^(2)=c^(2)`, where
`a` and
`b` are the shorter sides, and
`c` is the longer side of the triangle.

the x- and y-distances are
`a` and
`b`. We want to find the value of c, since that is the distance between the two points. So, plugging the known values into the Pythagorean Theorem,

`11^(2)+13^(2)=c^(2)`

`121+169=c^(2)`

`290=c^(2)`

`c\approx 16.1245154966`

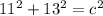
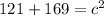
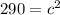
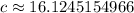
So, the distance between the two points is roughly 16.