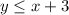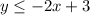Question

The graph below represents which system of inequalities?

graph of two infinite lines that intersect at a point. One line is solid and goes through the points negative 3, 0, negative 4, negative 1 and is shaded in below the line. The other line is solid, and goes through the points 1, 1, 2, negative 1 and is shaded in below the line.

Answer 1

The system of inequalities is

`y\leq x+3`

`y\leq -2x+3`

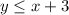
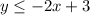
Explanation:

step 1

Find the equation of the solid line that goes through the points negative 3, 0, negative 4, negative 1

Let

A(-3,0),B(-4,-1)

Find the slope

m=(-1-0)/(-4+3)

m=-1/-1=1

The equation of the line into point slope form is equal to

y-y1=m(x-x1)

we have

m=1

point A(-3,0)

substitute

y-0=(1)(x+3)

y=x+3

The solution is the shaded area below the solid line

therefore

The equation of the first inequality is equal to

`y\leq x+3`

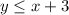
step 2

Find the equation of the solid line that goes through the points 1, 1, 2, negative 1

Let

C(1,1),D(2,-1)

Find the slope

m=(-1-1)/(2-1)

m=-2/1=-2

The equation of the line into point slope form is equal to

y-y1=m(x-x1)

we have

m=-2

point C(1,1)

substitute

y-1=(-2)(x-1)

y=-2x+2+1

y=-2x+3

The solution is the shaded area below the solid line

therefore

The equation of the first inequality is equal to

`y\leq -2x+3`

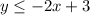
therefore

The system of inequalities is

`y\leq x+3`

`y\leq -2x+3`