Answer:
1.
 ,
,
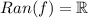 .
.
2.
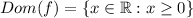 ,
,
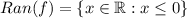 .
.
Explanation:
1. Since the degree of the radical is an odd number, the radicand can be any real number, then
 can take any real value, so the domain of
can take any real value, so the domain of
 is the set of all real numbers,
is the set of all real numbers,
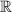 .
.
Now, if
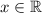 , then
, then
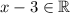 , so
, so
![\sqrt[3]{x-3} \in \mathbb{R}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dctzmvxccwdhd9cdanv0qcgqkl4hmgxe1j.png) , and thus
, and thus
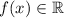 , which leads us to affirm that the range of
, which leads us to affirm that the range of
 is the set of all real numbers,
is the set of all real numbers,
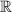 .
.
2. Since the degree of the radical is an even number, the radicand can not be a negative number, then
 can take only nonnegaive values, so the domain of
can take only nonnegaive values, so the domain of
 is the set of all nonnegative numbers,
is the set of all nonnegative numbers,
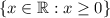 .
.
Now, if
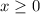 , then
, then
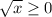 so
so
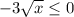 , and thus
, and thus
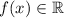 , which leads us to affirm that the range of
, which leads us to affirm that the range of
 is the set of all nonpositive numbers,
is the set of all nonpositive numbers,
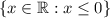 .
.