Answer:
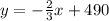
gradient = =
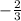
y-intercept =
Explanation:
• The slope-intercept form of an equation takes the general form:
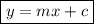 ,
,
where:
m = slope,
c = y-intercept.
• We are given the equation:
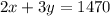
To change this into the slope-intercept form, we must make y the subject:
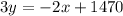 [subtract
[subtract
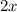 from both sides]
from both sides]
⇒
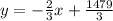 [divide both sides by 3]
[divide both sides by 3]
⇒
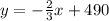
• Comparing this equation with the general form equation, we see that:
m =
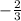
c =
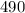 .
.
This means that the gradient is
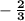 , and the y-intercept is
, and the y-intercept is
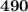 .
.