Question

The temperature of 6.24 L of a gas is increased from 25.0°C to 55.0°C at constant pressure. The new volume of the gas is Question 18 options: 2.84 L. 6.87 L. 13.7 L. 5.67 L.

Answer 1

Heating this gas to 55 °C will raise its volume to 6.87 liters.

Assumption: this gas is ideal.

Step-by-step explanation:

By Charles's Law, under constant pressure the volume
`V` of an ideal gas is proportional to its absolute temperature
`T` (the one in degrees Kelvins.)

Alternatively, consider the ideal gas law:

`\displaystyle V = (n \cdot R)/(P)\cdot T`.

• 
  `n` is the number of moles of particles in this gas.
  `n` should be constant as long as the container does not leak.
• 
  `R` is the ideal gas constant.
• 
  `P` is the pressure on the gas. The question states that the pressure on this gas is constant.

Therefore the volume of the gas is proportional to its absolute temperature.

Either way,

`V\propto T`.

`\displaystyle V_2 = V_1\cdot (T_2)/(T_1)`.

For the gas in this question:

• Initial volume:
  `V_1 = \rm 6.24\; L`.

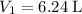Convert the two temperatures to degrees Kelvins:

• Initial temperature:
  `T_1 = \rm 25.0\;\textdegree{C} = (25.0 + {\rm 273.15})\; K = 298.15\;K`.
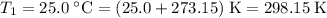• Final temperature:
  `T_1 = \rm 55.0\;\textdegree{C} = (55.0 + {\rm 273.15})\; K = 328.15\;K`.

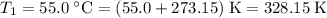Apply Charles's Law:

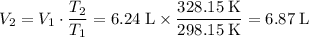`\displaystyle V_2 = V_1\cdot (T_2)/(T_1) = \rm 6.24\;L * (328.15\; K)/(298.15\;K) = 6.87\;L`.