Question

What are the zeros of the function f(x) = x^2 + 2x- 8 / x^2 - 2x - 8

Answer 1

x=-4 and x=2

Explanation:

You are given the function

`f(x)=(x^2+2x-8)/(x^2-2x-8)`

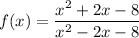
The zeros of the function are those value of x, for which
`f(x)=0`

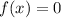
First, find x for which function is undefined

`x^2-2x-8\\eq0\\ \\x^2-4x+2x-8\\eq 0\\ \\x(x-4)+2(x-4)\\eq 0\\ \\(x-4)(x+2)\\eq 0\\ \\x\\eq 4\text{ and }x\\eq -2`

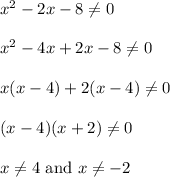
Now find points at which f(x)=0:

`f(x)=0\Rightarrow x^2+2x-8=0\\ \\x^2+4x-2x-8=0\\ \\x(x+4)-2(x+4)=0\\ \\(x-2)(x+4)=0\\ \\x=2\text{ or }x=-4`

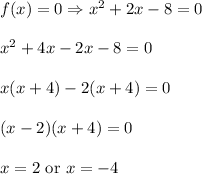
For both these values (x=-4 and x=2) function f(x) is defined, then x=-4 and x=2 are zeros of the function.