Question

An anthropologist finds that a prehistoric bone contains less than 8.1% of the amount of Carbon-14 the bones would have contained when the person was alive. How long ago did the person die? (The constant for Carbon-14 is 0.00012.)

19,000 years

20,944 years

21,048 years

23,028 years

Answer 1

20,944 years

Explanation:

The formula you use for this type of decay problem is the one that uses the decay constant as opposed to the half life in years. We are given the k value of .00012. If we don't know how much carbon was in the bones when the person was alive, it would be safer to say that when he was alive he had 100% of his carbon. What's left then is 8.1%. Because the 8.1% is left over from 100% after t years, we don't need to worry about converting that percent into a decimal. We can use the 8.1. Here's the formula:

`N(t)=N_(0) e^(-kt)`

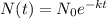
where N(t) is the amount left over after the decay occurs,
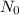`N_(0)` is the initial amount, -k is the constant of decay (it's negative cuz decay is a taking away from as opposed to a giving to) and t is the time in years. Filling in accordingly,

`8.1=100e^(-.00012t)`

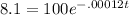
Begin by dividing the 100 on both sides to get

`.081=e^(-.00012t)`

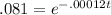
Now take the natural log of both sides. Since the base of a natual log is e, natural logs and e "undo" each other, much like taking the square root of a squared number.

ln(.081)= -.00012t

Take the natual log of .081 on your calculator to get

-2.513306124 = -.00012t

Now divide both sides by -.00012 to get t = 20,944 years