Question

A person invests $1,150 in an account that earns 5% annual interest compounded continuously. Find when the value of the investment reaches $2,000. If necessary round to the nearest tenth.

The investment will reach a value of $2,000 in approximately_____years.

Answer 1

11.1 years

Explanation:

The formula for interest compounding continuously is:

`A(t)=Pe^(rt)`

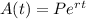
Where A(t) is the amount after the compounding, P is the initial deposit, r is the interest rate in decimal form, and t is the time in years. Filling in what we have looks like this:

`2000=1150e^{{.05t}`

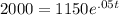
We will simplify this first a bit by dividing 2000 by 1150 to get

`1.739130435=e^(.05t)`

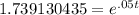
To get that t out the exponential position it is currently in we have to take the natural log of both sides. Since a natural log has a base of e, taking the natual log of e cancels both of them out. They "undo" each other, for lack of a better way to explain it. That leaves us with

ln(1.739130435)=.05t

Taking the natural log of that decimal on our calculator gives us

.5533852383=.05t

Now divide both sides by .05 to get t = 11.06770477 which rounds to 11.1 years.