Answer:
a.
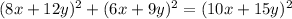
b.
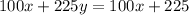 Which means it is an identity
Which means it is an identity
Explanation:
The Pythagorean Theorem states that in every right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the respective lengths of the legs. It is the best-known proposition among those that have their own name in mathematics.
If in a right triangle there are legs of length a, and b, and the measure of the hypotenuse is c, then The following relationship is fulfilled:

a. Write an equation using the Pythagorean Theorem and the measurements provided in the diagram
From the exercise shown in the image, we can get the values of a, b, and c.
a = 8x+12y, b = 6x+9y, and c = 10x+15y
Write an equation using the Pythagorean Theorem
We obtain:
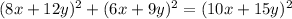
b. Transform each side of the equation to determine if it is an identity.
In mathematics, an identity is the realization that two objects that are mathematically written differently, are in fact the same object. In particular, an identity is an equality between two expressions, which is true whatever the values of the different ones are.
So, we transform each side of the equation
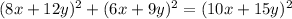
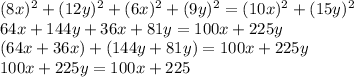 Which means it is an identity
Which means it is an identity
.