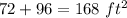Answer:
The answer in the attached figure
Explanation:
step 1
Find the area of one blue square
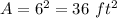
step 2
Find the area of one orange triangle
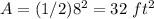
Part 1)
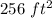
Divide the total area by the area of one orange triangle
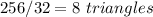
Part 2)
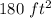
Divide the total area by the area of one blue square
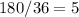
Part 3)
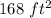
Let
x----> the number of blue squares
y ------> the number of orange triangles
we know that
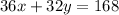
Construct a table and prove different values for x and for y
we have
x=2, y=3
Two blue squares and three orange triangles
Area of blue squares
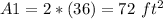
Area of an orange triangles
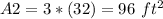
so
the area total is