Question

6. Describe the end behavior and determine

whether the graph represents an
odd-degree or an even-degree polynomial function. Then state the number of real 0s



7. GEOMETRY Recall the formula for finding the area of a rectangle Define a
variable for the width and set up an equation to find the dimensions of a rectangle with an area of 144 square inches given the length is 10 inches longer than the width

Answer 1

6. Since, by given graph,

The end behavior of the function f(x),

`f(x)\rightarrow -\infty\text{ if }x\rightarrow -\infty`

`f(x)\rightarrow +\infty\text{ if }x\rightarrow +\infty`

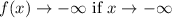
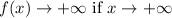
Thus, the function f(x) must has odd number of roots ( where the graph of a function intersects the x-axis )

⇒ The function must has odd number of solutions,

Again by the graph,

Graph of the function intersects the x-axis 5 times ( it touches the origin so it have the repeated root of x = 0 ),

Hence, the total number of real solution of f(x) is 5.

7. Let x represents the width of the rectangle( in inches ),

Given,

The length is 10 inches longer than the width,

⇒ Length of the rectangle = ( x + 10 ) inches

Thus, the area of the rectangle,

A = length × width = x(x+10)

According to the question,

A = 144 in²

⇒ x(x+ 10) = 144

`x^2+10x=144`

`x^2+10x-144=0`

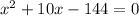
`x^2+18x-8x-144=0` ( Middle term splitting )

`x(x+18)-8(x+18)=0`

`(x+18)(x-8)=0`

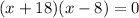
⇒ x = -18 or x = 8 ( By zero test property )

The width can not be negative,

Hence, the width of the rectangle would be 8 inches.

Answer 2

6. an odd-degree polynomial function.

f(x)⇒-∞ as x⇒-∞ and f(x)⇒∞ as x⇒∞

7. Length =x+10=8+10=18 inches

Width=x=8 inches

Step by step explanation;

6. The graph represent an odd-degree polynomial function.

The graph enters the graphing box from the bottom and goes up leaving through the top of the graphing box.This is a positive polynomial whose limiting behavior is given by;

f(x)⇒-∞ as x⇒-∞ and f(x)⇒∞ as x⇒∞

7.

The area of a rectangle is given by l×w, where l is length and w is the width

Let=w=x , l=x+10 and A=144 in² then;

l×w=144

(x+10) × x = 144

x²+10x =144......................complete squares on both sides

x²+10x+25=144+25

x²+10x+25=144+25................factorize

(x+5)²=169.......................square root the right-hand side

x+5= ±√169

x+5=±13.

x+5=13⇒⇒⇒x=8

x+5=-13⇒⇒⇒x= --18

x=8 inches....................value of width should be positive

Length =x+10=8+10=18 inches

Width=x=8 inches