Question

PLEASE HELP ME PLEASE I BEG YOU

A subscription-based website sends out email reminders to 15,000 customers whose subscriptions are due to be renewed, inviting them to renew at a discount. After the email is sent, the number of customers whose subscriptions are due to be renewed decreases at a rate that compounds hourly, for a per-day decrease of 14.4%. The number of such customers after n days is given by the expression below.


15,000(1-0.144/24)∧24n


What does (1-0.144/24) represent?


A. the change per hour in the number of customers whose subscriptions are due to be renewed


B. the number of customers whose subscriptions are still due to be renewed after one day


C. the initial number of customers whose subscriptions are due to be renewed


D. the decay rate, which reveals the hourly rate of change in the number of customers whose subscriptions are due to be renewed

Answer 1

I think it's B.

Explanation:

Because the equation is 1 - 0.144/24 should represent the amount of emails to be answered after one day.

Answer 2

D. The decay rate, which reveals the hourly rate of change in the number of customers whose subscriptions are due to be renewed.

Explanation:

An exponential decay function is,

`f(x)=a(1-r)^x`

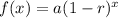
Where, a is initial value,

r is rate of change per period,

x is the number of periods,

(1-r) is decay factor that shows the periodic rate of change in the initial value.

Given expression that represents the number of such customers after n days is,

`15,000(1-(0.144)/(24))^(24n)`

By comparing,

15,000 is the initial number of customers who are due to be renewed,

`(0.144)/(24)` is the change per hour in the number of customers,

24n is the total number of hours,

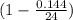`(1-(0.144)/(24))` is the decay factor or decay rate that reveals the hourly rate of change in the number of customers,

Hence, option 'D' is correct.