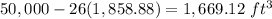Question

Part 6

want to line the front of the school with cylinder shaped beams filled with moon sand. Each beam is 37 feet tall with a diameter of 8 feet.

What is the total volume of each beam?

You are given a container with a 50,000 sq ft of sand for your beams.

1. How many beams can you fill with this sand?

2. Will you have any sand left over? If so how much?

What did you do to get your answers to question 1 and 2? Describe your work in detail.​

Answer 1

Part 1) The volume of each beam is
`1,858.88\ ft^(3)`

Part 2) You can fill
`26\ beams`

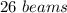
Part 3) Yes, the amount of sand left over is
`1,669.12\ ft^(3)`

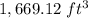
Explanation:

Part 1) What is the total volume of each beam?

The volume of a cylinder is equal to

`V=\pi r^(2) h`

we have

`h=37\ ft`

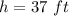
`r=8/2=4\ ft` ----> the radius is half the diameter

assume

`\pi=3.14`

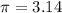
substitute the values

`V=(3.14)(4)^(2) (37)`

`V=1,858.88\ ft^(3)`

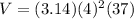
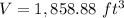
Part 2) How many beams can you fill with this sand?

we know that

You are given a container with a 50,000 sq ft of sand for your beams

Note Is a 50,000 cubic foot of sand instead of 50,000 sq ft of sand

Divide the total volume of sand by the volume of each beam to obtain the number of beams

`50,000/1,858.88=26.9\ beams`

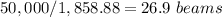
Round down

`26.9=26\ beams`

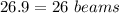
Part 3) Will you have any sand left over? If so how much?

yes

`50,000-26(1,858.88)=1,669.12\ ft^(3)`