Part A
The scatterplot is shown the attachment.
Part B
Using a linear regression equation that models Patrick's referrals has a positive slope.
This means that, there is a positive relation between time(number of days),x and the number of personal recommendations, y.
In other words, as the number of days increases, the number of personal recommendations also increases.
Question 2.
The given functions are:
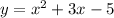
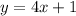
To find the point where the graphs of these functions intersect,we solve the two equations simultaneously.
We equate the two equations to get:
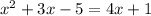
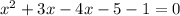
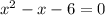
Factor to obtain:
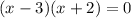
x=3 and x=-2
We put x=-2, into
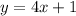 to get;
to get;
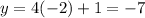
when x=3
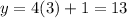
Therefore the graphs intersect at (-2,-7) and(3,13).
Yes, solution is correct.