Question

A dog chases a squirrel. The dog is originally 200 feet away from the squirrel. The dog's speed is 150 feet per minute. The squirrel's speed is 100 feet per minute. How long will it take for the dog to get the squirrel?

Answer 1

4 mins

Explanation:

Let x = the distance the squirrel runs before it's caught,

then the dog runs 200 + x.

distance/rate = time

x/100 = (200+x)/150 =>x/2 = (200+x)/3 => 400 +2x = 3x => x = 400

The squirrel runs 400' in 4 minutes.

Answer 2

15 seconds

Explanation:

If you make a table of values for the dog and the squirrel using d = rt, then the rates are easy: the dog's rate is 150 and the squirrel's is 100. The t is what we are looking for, so that's our unknown, and the distance is a bit tricky, but let's look at what we know: the dog is 200 feet behind the squirrel, so when the dog catches up to the squirrel, he has run some distance d plus the 200 feet to catch up. Since we don't know what d is, we will just call it d! Now it seems as though we have 2 unknowns which is a problem. However, if we solve both equations (the one for the dog and the one for the squirrel) for t, we can set them equal to each other. Here's the dog's equation:

d = rt

d+200 = 150t

And the squirrel's:

d = 100t

If we solve both for t and set them equal to each other we have:

`(150)/(d+200) =(100)/(d)`

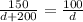
Now we can cross multiply to solve for d:

150d = 100d + 20,000 and

50d = 20,000

d = 400

But we're not looking for the distance the squirrel traveled before the dog caught it, we are looking for how long it took. So sub that d value back into one of the equations we have solved for t and do the math:

`t=(100)/(d)=(100)/(400) =(1)/(4)`

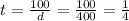
That's 1/4 of a minute which is 15 seconds.