Question

Find z 1 ÷ z 2 for z 1 = 9(cos225° + isin225°) and z 2 = 3(cos45° + isin45°).

Express the quotient in a + bi form.

Answer 1

-1

Explanation:

Use DeMoivre's Theorem for division of complex polar numbers. Set it up like this:

`(9(cos225+sin225i))/(3(cos45+sin45i))`

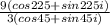
The rule is

`(z_(1) )/(z_(2) )cis(\theta_(1)-\theta _(2) )`

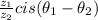
Our z1 is 9 and our z2 is 3, so the division of those gives you 3. The subtraction of the angles 225 - 45 = 180, therefore:

3 cis 180° = 3(cos 180 + sin 180 i)

The cos of 180 is -1 and the sin of 180 is 0, so 3(-1 + 0) = -3

Answer 2

`\bf \qquad \textit{division of two complex numbers} \\\\ \cfrac{r_1[cos(\alpha)+isin(\alpha)]}{r_2[cos(\beta)+isin(\beta)]}\implies \cfrac{r_1}{r_2}[cos(\alpha - \beta)+isin(\alpha - \beta)] \\\\[-0.35em] \rule{34em}{0.25pt}`

`\bf \begin{cases} z1=9[cos(225^o)+i~sin(225^o)]\\\\ z2=3[cos(45^o)+i~sin(45^o)] \end{cases}\implies \cfrac{z1}{z2}\implies \cfrac{9[cos(225^o)+i~sin(225^o)]}{3[cos(45^o)+i~sin(45^o)]} \\\\\\ \cfrac{9}{3}[cos(225^o-45^o)+isin(225^o-45^o)]\implies 3[cos(180^o)+i~sin(180^o)] \\\\\\ 3[(-1)+i~(0)]\implies -3+0i`