Question

Which is the correct letter answer of the value of the log equation?

Answer 1

The value of the single logarithm is -11 ⇒ answer B

Explanation:

* Lets revise the rule of the logarithmic functions

# ㏒ a + ㏒ b = ㏒ ab

# ㏒ a - ㏒ b = ㏒ a/b

# ㏒ a^n = n ㏒ a

# ㏒ 1 = 0

* Now lets solve the problem

∵
`log_(b)((A^(5)C^(2))/(D^(6)))`

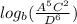
- Change the single logarithm to an expression by change the

multiplication to addition and the division to subtraction

∵
`log_(b)A^(5)=5log_(b)A`

∵
`log_(b)C^(2)=2log_(b)C`

∵
`log_(b)D^(6)=6log_(b)D`

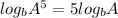
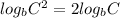
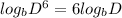
∴ The single logarithm =
`5log_(b)A+2log_(b)C-6log_(b)D`

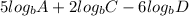
* Now lets substitute the values

∵
`log_(b)A=3;===log_(b)C=2;===log_(b)D=5`

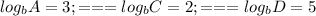
- Substitute the values into the expression

∴ The value = 5(3) + 2(2) - 6(5) = 15 + 4 - 30 = -11

* The value of the single logarithm is -11