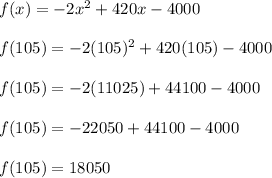Answer:
The company's maximum monthly profit is $18050
Explanation:
First we need to distribute everything in order to solve for the maximum
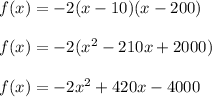
Now we can use the equation
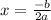 in order to find the x-value of the maximum
in order to find the x-value of the maximum
From our function, we know that a=-2 and b=420
We can plug in these values and solve for x to get
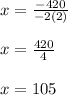
Now we can plug our x-value into our function in order to find the maximum monthly profit