The limit of sqrt(9x^4 + 1)/(x^2 - 3x + 5) as x approaches infinity is \displaystyle\lim_(x \to \infty) (√(9x^4+1))/(x^2 -3x + 5) (A) 1 (B) 3 (C) 9 (D) nonexistent

Question

The limit of sqrt(9x^4 + 1)/(x^2 - 3x + 5) as x approaches infinity is


`\displaystyle\lim_(x \to \infty) (√(9x^4+1))/(x^2 -3x + 5)`


(A) 1

(B) 3

(C) 9

(D) nonexistent

Answer 1

The limit of
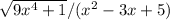`\(√(9x^4 + 1)/(x^2 - 3x + 5)\)` as x approaches infinity is 3, after comparing the highest powers of x in both the numerator and the denominator and simplifying.

Step-by-step explanation:

To find the limit of the given function
`\(\displaystyle\lim_(x \to \infty) (√(9x^4+1))/(x^2 -3x + 5)\)` as x approaches infinity, we can use the property of limits involving infinity. We need to compare the highest powers of x in both the numerator and the denominator. The highest power of x in the numerator under the square root is x⁴, and outside the square root, it will be x². In the denominator, the highest power is x². If we divide the numerator and the denominator by x², we get:

`\[ (√(9x^4+1))/(x^2 -3x + 5) = \frac{\sqrt{(9x^4)/(x^4)+(1)/(x^4)}}{(x^2)/(x^2) -(3x)/(x^2) + (5)/(x^2)} = \frac{\sqrt{9+(1)/(x^4)}}{1 -(3)/(x) + (5)/(x^2)} \]`

As x approaches infinity, the terms
`\((1)/(x^4)\), \((3)/(x)\), and \((5)/(x^2)\)` approach zero, and we are left with:

`\[ (√(9))/(1) = 3 \]`

Therefore, the limit of the given function as x approaches infinity is 3, which corresponds to option (B).

Answer 2

B. 3.

Step-by-step explanation:

At the limit we can take the numerator to be √(9x^4) = 3x^2

The function is of the form ∞/ ∞ as x approaches ∞ so we can apply l'hopitals rule:

Differentiating top and bottom we have 6x / 2x - 3. Differentiating again we get 6 / 2 = 3.

Our limit as x approaches infinity is 3.