Question

The statement tan theta -12/5, csc theta -13/12, and the terminal point determined by theta is in quadrant 2."

Answer 1

Answer is C. This is because in quadrant 2,
`\sin\theta>0` so
`\csc\theta>0` is also true.

Answer 2

Answer with explanation:

Let , Theta =A

`\tan A=(-12)/(5)\\\\ \csc A=(-13)/(12)`

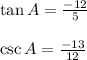
In First Quadrant all Trigonometric Function are Positive.

→In Quadrant,II , Sine and Cosecant , Function are Positive only.

→Cosecant theta is negative.So, Terminal point can't be in Second Quadrant.

Option C: