Answer
1)
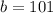
2)

3)
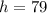
4)
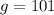
5)
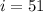
6)

Explanation
From the diagram,
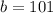 , corresponding angles are equal.
, corresponding angles are equal.
From the diagram, m=k, corresponding angles are equal.
But k+130=180, angles on a straight line sum up to 180 degrees.
This implies that k=180-130=50
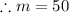
From the diagram ;
 ,angles on a straight line sum up to 180 degrees.
,angles on a straight line sum up to 180 degrees.
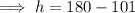
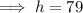
From the diagram,
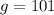 vertically opposite angles are equal.
vertically opposite angles are equal.
From the triangular portion;
i+h+m=180. sum of interior angles of a triangle.
This implies that:
i+79+50=180
i+129=180
i=180-129
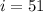
Finally
 , vertically opposite angles are equal.
, vertically opposite angles are equal.