For this case we have the following functions:
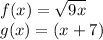
We must find

By definition of composition of functions we have to:

So:
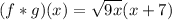
The domain of the function is given by all the values for which the function is defined. The function is defined for all real numbers greater than or equal to 0. That is:
[0, ∞)
Answer:
The zero is the smallest value of the domain