Question

What is the amplitude, period, and phase shift of f(x) = −4 sin(2x + π) − 5?

Amplitude = −4; period = 2π; phase shift: x = -pie/2
Amplitude = −4; period = π; phase shift: x = pie/2
Amplitude = 4; period = π; phase shift: x = -pie/2
Amplitude = 4; period = 2π; phase shift: x = pie/2

Answer 1

Amplitude = 4; period = π; phase shift: x = -pie/2

Explanation:

For a sine wave of the following type:

y = Asin(Bx + C) + D, we have that:

A represents the amplitude

C represents the phase shift

D represents the vertical shift

And the period is given by:
`(2 \pi)/(B)`

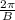
Therefore, considering: f(x) = −4 sin(2x + π) − 5, we know that sin(a + π) = -sin(a). Then:

f(x) = −4 sin(2x + π) − 5 = 4sin(2x)-5 = 4cos(2x - π/2) - 5

The amplitude equals 4

The period is T = π

The fase shift is: -π/2.

Therefore, the correct option is:

Amplitude = 4; period = π; phase shift: x = -pie/2