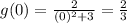Question

Identify the relative maximum value of g(x) for the function shown below

g(x) = 2/ x^2 +3

Answer 1

The relative maximum value is
`(2)/(3)`

Explanation:

The given function is

`g(x)=(2)/(x^2+3)`

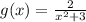
We differentiate to obtain;

`g'(x)=-(4x)/((x^2+3)^2)`

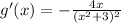
At turning points
`g'(x)=-(4x)/((x^2+3)^2)=0`

`\implies x=0`

`g''(x)=(16x^2)/((x^2+3)^3)- (4)/((x^2+3)^2)`

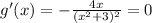
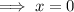
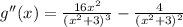
We apply the second derivative test to obtain:

`g''(0)=(16(0)^2)/(((0)^2+3)^3)- (4)/(((0)^2+3)^2)=-(4)/(9)`

Since the second derivative is negative, there is a relative maximum at x=0.

We substitute x=0 into the original function to obtain the relative maximum value.

`g(0)=(2)/((0)^2+3)=(2)/(3)`