Answer:

Explanation:
we know that
The volume of the silo is equal to the volume of a cylinder plus the volume of a hemisphere
so
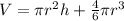
In this problem we have
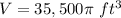
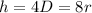 ----> 4 times the diameter is equal to 8 times the radius
----> 4 times the diameter is equal to 8 times the radius
substitute in the formula and solve for r
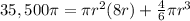
Simplify pi
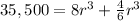
![35,500=r^(3)[8+(4)/(6)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hbu4qgt3lkqly89r30k85pghm2gehwi5o5.png)
![35,500=r^(3)[(52)/(6)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/h9gdkcsj08jtnihmev1qs7b0t1g5gfghv5.png)
![r^(3)=35,500/[(52)/(6)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/779e0x4te5ymkd4ly3zutkv4h12fzre4pq.png)
